P10. Càlcul MCCSS (Juny 2017 B)

Apartat a.-

Primerament estudiem ]  Buits (1): JXUwMDY4 ,] perquè el primer tros de la funció és un polinomi i sempre existeix en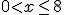 

El segon tros és continua en el seu interval de definició ja que el denominador s'anul·la en  1 i en  Buits (2): JXUwMDc1JXUwMDFj  

Estudiem la continuïtat de la funció 

Cada tros per separat és continua en el seu interval de definició, cal estudiar la continuïtat en  . Vegem que 0' Buits (3): JXUwMDY5JXUwMDA5  

Calculem 0' Buits (4): JXUwMDY5JXUwMDA5   i 0' Buits (5): JXUwMDY5JXUwMDA5   Per tant  és contínua en ] Buits (6): JXUwMDY4 ,  [  

Apartat b.-

Estudiem la monotonia de la funció. Calculem 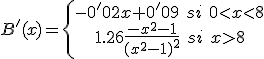 Per saber si la funció és derivable en  

Estudiem -0' Buits (7): JXUwMDY4JXUwMDA3   i  -0' Buits (8): JXUwMDY4JXUwMDAy

Com les derivades laterals no són iguals, la funció  no és derivable en  Buits (9): JXUwMDYw  . Estudiem la monotonia de la funció 

Com vegem, la funció és creixent a l'interval ] Buits (10): JXUwMDY4 , 4'5 [ i decreixent a l'interval ] Buits (11): JXUwMDZjJXUwMDEzJXUwMDEy ,[

Apartat c.- 

Com vegem el màxim benefici s'assoleix en el punt ( Buits (12): JXUwMDZjJXUwMDEzJXUwMDEy , 0'302 )

Com parlem de milers d'euros s'haurà d'invertir Buits (13): JXUwMDZjJXUwMDAxJXUwMDA1JXUwMDAw € per obtenir un benefici de Buits (14): JXUwMDZiJXUwMDAzJXUwMDAy €

Apartat d.- 

Com vegem a la gràfica, obtendriem, com a mínim, un benefici de Buits (15): JXUwMDZhJXUwMDAy €. És així perquè