
Apartat a.-
Expresem la recta  en la seua forma paramètrica. Així tenim
en la seua forma paramètrica. Així tenim 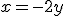 i
i 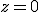 La forma paramètrica és
La forma paramètrica és 
El seu vector director és 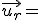 (
JXUwMDc1JXUwMDFm
,
JXUwMDY5
,
JXUwMDY4
) que serà el vector associat al pla solució. El pla demanat queda determinat per
(
JXUwMDc1JXUwMDFm
,
JXUwMDY5
,
JXUwMDY4
) que serà el vector associat al pla solució. El pla demanat queda determinat per 
La seua equació és 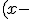 JXUwMDZh
,
JXUwMDZh
,  ,
, 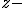 JXUwMDY5
JXUwMDY5
 ·(
JXUwMDc1JXUwMDFm
,
JXUwMDY5
,
JXUwMDY4
)=
JXUwMDY4
. Desenvolupant tenim
·(
JXUwMDc1JXUwMDFm
,
JXUwMDY5
,
JXUwMDY4
)=
JXUwMDY4
. Desenvolupant tenim  JXUwMDc1JXUwMDFm
JXUwMDc1JXUwMDFm
 JXUwMDZj
=
JXUwMDY4
JXUwMDZj
=
JXUwMDY4
Apartat b.-
El punt 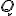 de tall entre la recta i el pla queda determinat pel sistema
de tall entre la recta i el pla queda determinat pel sistema 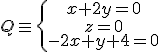 que és compatible determinat.
que és compatible determinat.
Calculant la solució, tindrem 
Apartat c.-
La distància demanada és 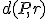 . Per calcular-la hem de calcular un punt
. Per calcular-la hem de calcular un punt  .
.
Si en la equació paramètrica de la recta  fem
fem  , tindrem que
, tindrem que  JXUwMDY4
,
JXUwMDY4
,
JXUwMDY4
JXUwMDY4
,
JXUwMDY4
,
JXUwMDY4
 i
i
Així el vector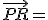 (
JXUwMDc1JXUwMDFm
,
JXUwMDY4
,
JXUwMDc1JXUwMDFj
) i
(
JXUwMDc1JXUwMDFm
,
JXUwMDY4
,
JXUwMDc1JXUwMDFj
) i  (
JXUwMDY5
,
JXUwMDZh
,
JXUwMDc1JXUwMDFm
). Tindrem que
(
JXUwMDY5
,
JXUwMDZh
,
JXUwMDc1JXUwMDFm
). Tindrem que 
La distància del punt  a la recta
a la recta  és la menor distància que hi ha entre el punt
és la menor distància que hi ha entre el punt  i la recta
i la recta  . Per tant si
. Per tant si 