Apartat a.-
Expresem la recta  en forma implícita
en forma implícita  JXUwMDc1JXUwMDFl
JXUwMDc1JXUwMDFl
 JXUwMDYw
i
JXUwMDYw
i  JXUwMDc1JXUwMDFm
JXUwMDc1JXUwMDFm
 JXUwMDZl
JXUwMDZl
Volem calcular la recta  sabent que
sabent que  Calcularem un punt
Calcularem un punt 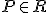 de forma que
de forma que  on
on  és director de la recta
és director de la recta 
 El punt genèric de la recta és
El punt genèric de la recta és  per tant
per tant  (
( -
JXUwMDZk
,
JXUwMDc1JXUwMDFl
-
JXUwMDZk
,
JXUwMDc1JXUwMDFl
 +
JXUwMDY5
,
JXUwMDc1JXUwMDFm
+
JXUwMDY5
,
JXUwMDc1JXUwMDFm
 +
JXUwMDZi
) i
+
JXUwMDZi
) i 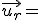 (
JXUwMDc1JXUwMDFj
,
JXUwMDZi
,
JXUwMDZh
)
(
JXUwMDc1JXUwMDFj
,
JXUwMDZi
,
JXUwMDZh
)
Si  aleshores
aleshores  JXUwMDY4
Així tenim
JXUwMDY4
Així tenim  i per tant
i per tant  JXUwMDY5
JXUwMDY5
El punt  (
JXUwMDY5
,
JXUwMDZk
,
JXUwMDZj
) i
(
JXUwMDY5
,
JXUwMDZk
,
JXUwMDZj
) i  JXUwMDc1JXUwMDFm
,
JXUwMDY5
JXUwMDc1JXUwMDFm
,
JXUwMDY5
 . L'equació vectorial de la recta demanada és
. L'equació vectorial de la recta demanada és  (
JXUwMDZk
,
JXUwMDZm
,
JXUwMDZi
)+
(
JXUwMDZk
,
JXUwMDZm
,
JXUwMDZi
)+ ( 4 ,
JXUwMDZh
,
JXUwMDc1JXUwMDFj
) on
( 4 ,
JXUwMDZh
,
JXUwMDc1JXUwMDFj
) on 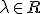
Apartat b.-
Ens demanen  o el que és el mateix
o el que és el mateix 
Apartat c.-

Calculem el pla  la seua equació serà (
la seua equació serà ( JXUwMDZi
,
JXUwMDZi
,  JXUwMDY5
,
JXUwMDY5
,  )·(
JXUwMDc1JXUwMDFj
,
JXUwMDZi
,
JXUwMDZh
)=
JXUwMDY4
.
)·(
JXUwMDc1JXUwMDFj
,
JXUwMDZi
,
JXUwMDZh
)=
JXUwMDY4
.
Desenvolupant tenim  JXUwMDZi
JXUwMDZi
 JXUwMDZh
JXUwMDZh
 JXUwMDZl
JXUwMDZl
 JXUwMDY4
JXUwMDY4
Ens demanen 