Apartat a.-

Si  és l'hipotenusa del triangle, l'angle recte del triangle està al vètex
és l'hipotenusa del triangle, l'angle recte del triangle està al vètex  així que els vectors
així que els vectors  i
i  són perpendiculars i
són perpendiculars i  JXUwMDY4
JXUwMDY4
Com  (
JXUwMDZi
,
JXUwMDY5
,
JXUwMDZk
-
(
JXUwMDZi
,
JXUwMDY5
,
JXUwMDZk
-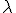 ) i
) i  (
JXUwMDY5
,
JXUwMDZh
,
JXUwMDc1JXUwMDFm
) , tenim
(
JXUwMDY5
,
JXUwMDZh
,
JXUwMDc1JXUwMDFm
) , tenim  JXUwMDZh
JXUwMDZh
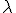 -
JXUwMDZj
. Per tant tindrem l'equació
JXUwMDZh
-
JXUwMDZj
. Per tant tindrem l'equació
JXUwMDZh
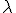 -
JXUwMDZj
=
JXUwMDY4
així
-
JXUwMDZj
=
JXUwMDY4
així  =
JXUwMDZh
=
JXUwMDZh
Apartat b.-
Si  tindrem
tindrem  (
JXUwMDc1JXUwMDFj
,
JXUwMDZh
,
JXUwMDZl
) ,
(
JXUwMDc1JXUwMDFj
,
JXUwMDZh
,
JXUwMDZl
) ,  (
JXUwMDZh
,
JXUwMDZi
,
JXUwMDZk
) i
(
JXUwMDZh
,
JXUwMDZi
,
JXUwMDZk
) i  (
JXUwMDZi
,
JXUwMDZk
,
JXUwMDZi
) .
(
JXUwMDZi
,
JXUwMDZk
,
JXUwMDZi
) .
Així  (
JXUwMDZi
,
JXUwMDY5
,
JXUwMDc1JXUwMDFj
) ,
(
JXUwMDZi
,
JXUwMDY5
,
JXUwMDc1JXUwMDFj
) , 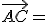 (
JXUwMDZj
,
JXUwMDZi
,
JXUwMDc1JXUwMDFl
) i
(
JXUwMDZj
,
JXUwMDZi
,
JXUwMDc1JXUwMDFl
) i  (
JXUwMDY4
,
JXUwMDZk
,
JXUwMDZk
)
(
JXUwMDY4
,
JXUwMDZk
,
JXUwMDZk
)
L'àrea del triangle és 
Apartat c.-
Si  sabem que
sabem que  (
JXUwMDc1JXUwMDFj
,
JXUwMDZh
,
JXUwMDZl
). Els vectors
(
JXUwMDc1JXUwMDFj
,
JXUwMDZh
,
JXUwMDZl
). Els vectors  (
JXUwMDZi
,
JXUwMDY5
,
JXUwMDc1JXUwMDFj
) i
(
JXUwMDZi
,
JXUwMDY5
,
JXUwMDc1JXUwMDFj
) i  (
JXUwMDZj
,
JXUwMDZi
,
JXUwMDc1JXUwMDFl
) són LI i són directors del pla
(
JXUwMDZj
,
JXUwMDZi
,
JXUwMDc1JXUwMDFl
) són LI i són directors del pla 
. El pla solució és  o siga
o siga 
La seua equació implícita és  JXUwMDY4
Desenvolupant tenim
JXUwMDY4
Desenvolupant tenim  JXUwMDYw
JXUwMDYw
 JXUwMDY4
JXUwMDY4