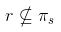Primerament calculem un punt i el vector director de cada recta.
Recta  d'ahí
d'ahí  així, expresada en forma paramètrica, tenim
així, expresada en forma paramètrica, tenim 
Si tindrem un punt de la recta és
tindrem un punt de la recta és  (
JXUwMDY4
,
JXUwMDZi
,
JXUwMDZh
) i el seu vector director és
(
JXUwMDY4
,
JXUwMDZi
,
JXUwMDZh
) i el seu vector director és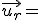 (
JXUwMDY5
,
JXUwMDY5
,
JXUwMDZh
)
(
JXUwMDY5
,
JXUwMDY5
,
JXUwMDZh
)
Recta  d'ahí
d'ahí 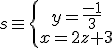 així, expresada en forma paramètrica, tenim
així, expresada en forma paramètrica, tenim 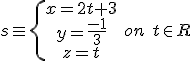
Si tindrem un punt de la recta és
tindrem un punt de la recta és  (
JXUwMDZi
,
(
JXUwMDZi
,  ,
JXUwMDY4
) i el seu vector director és
,
JXUwMDY4
) i el seu vector director és  (
JXUwMDZh
,
JXUwMDY4
,
JXUwMDY5
)
(
JXUwMDZh
,
JXUwMDY4
,
JXUwMDY5
)
Apartat a.-

Ens demanen el pla  o siga
o siga  La seua equació implicita serà
La seua equació implicita serà  JXUwMDY4
JXUwMDY4
Desenvolupant, tenim  JXUwMDZi
JXUwMDZi
 JXUwMDZh
JXUwMDZh
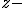 JXUwMDZk
JXUwMDZk
 JXUwMDY4
JXUwMDY4
Apartat b.-
La recta demanada és  El vector director de la recta
El vector director de la recta  serà
serà 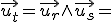 (
JXUwMDY5
,
JXUwMDZi
,
JXUwMDc1JXUwMDFm
)
(
JXUwMDY5
,
JXUwMDZi
,
JXUwMDc1JXUwMDFm
)
La seua equació vectorial serà  (
JXUwMDY4
,
JXUwMDY4
,
JXUwMDY4
)
(
JXUwMDY4
,
JXUwMDY4
,
JXUwMDY4
) (
JXUwMDY5
,
JXUwMDZi
,
JXUwMDc1JXUwMDFm
)
(
JXUwMDY5
,
JXUwMDZi
,
JXUwMDc1JXUwMDFm
)
Apartat c.-
El resoldrem de dues formes:
Primera.-
Si el pla  conté a la recta
conté a la recta  , el vector associat del pla i el vector director de la recta
, el vector associat del pla i el vector director de la recta  deurien ser perpendiculars.
deurien ser perpendiculars.
Com el vector associat del pla és el director de la recta  , ja que la recta és perpendicular al pla. Tendria que acomplir-se que
, ja que la recta és perpendicular al pla. Tendria que acomplir-se que  JXUwMDY4
JXUwMDY4
Però JXUwMDZj
JXUwMDZj
 JXUwMDY4
i per tant
JXUwMDY4
i per tant 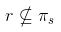
Segona.-

Calculem el pla que conté a  i és perpendicular a
i és perpendicular a 
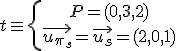
L'equació serà  (x , y-
JXUwMDZi
, z-
JXUwMDZh
)·(
JXUwMDZh
,
JXUwMDY4
,
JXUwMDY5
)=
JXUwMDY4
Per tant
(x , y-
JXUwMDZi
, z-
JXUwMDZh
)·(
JXUwMDZh
,
JXUwMDY4
,
JXUwMDY5
)=
JXUwMDY4
Per tant  2
2  JXUwMDZh
JXUwMDZh
 JXUwMDY4
JXUwMDY4
Aquest pla és prependicular a la recta  i conté a
i conté a  , per comprovar si conté a
, per comprovar si conté a  considerem un altre punt
considerem un altre punt  de la recta
de la recta  i comprovem si pertany o no al pla
i comprovem si pertany o no al pla  .
.
Si en la recta  ,
, 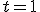 tindrem
tindrem  (
JXUwMDY5
,
JXUwMDZj
,
JXUwMDZj
) si substituim en l'equació del pla, tenim
(
JXUwMDY5
,
JXUwMDZj
,
JXUwMDZj
) si substituim en l'equació del pla, tenim  i per tant
i per tant